LLM Optimization: Lora and Qlora | Towards Data Science
With the advent of Chatgpt, the world recognized the powerful potential of large language models that could understand natural language and respond to user requests with high accuracy. In the abbreviation of LLM, the first letter l represent Bigreflects the large number of parameters that these models usually have.
Modern LLMs usually contain a billion parameters. Now, imagine a situation where we want to adapt LLM to downstream tasks. A common approach includes Fine adjustmentwhich involves adjusting the existing weights of the model in the new dataset. However, this process is very slow and resource-intensive, especially when running on local machines with limited hardware.
During the fine-tuning process, some neural network layers can be frozen to reduce the complexity of training, and this method is still insufficient due to the high computational cost.
To address this challenge, in this article, we will discuss Lola (low level adaptation)a popular technique that reduces computational load during fine-tuning of large models. As a bonus, we also look at Qlora, which is built on Lora by quantization to further increase efficiency.
Neural Network Representation
Let’s adopt a fully connected neural network. Each of its layers includes n Neurons are fully connected to m Neurons from the lower layer. There are a total of n Go for m It can be represented as a connection of matrices with various dimensions.

When a new input is passed to a layer, all we have to do is perform matrix multiplication between the weight matrix and the input vector. In fact, this operation is highly optimized using an advanced linear algebra library and is often performed simultaneously on the entire input to speed up the calculations.
Multiplication skills
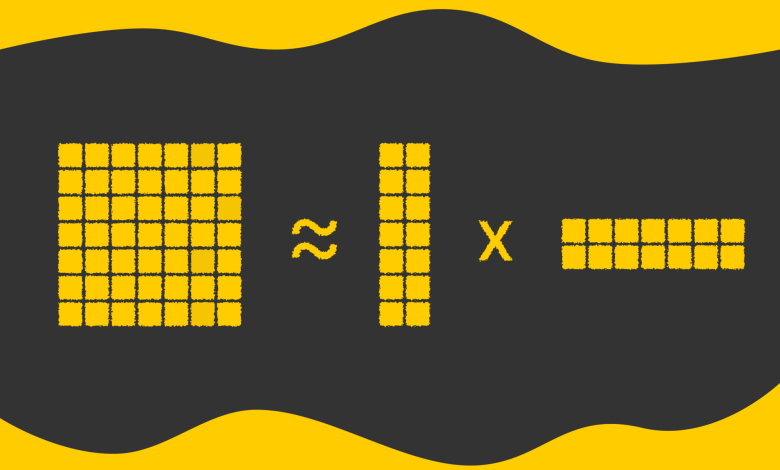
The weight matrix in a neural network can have extremely large dimensions. Instead of storing and updating the complete matrix, we can break it down into products of two smaller matrices. Specifically, if the weight matrix has dimensions n×mwe can approximate it using a matrix of two sizes n×k and K×mWhere k is a smaller inner dimension (k).
For example, suppose the original weight matrix is 8192×8192roughly corresponding 67m parameter. If we choose k = 8the decomposed version will contain two matrices: one of the size 8192×8 There is another 8×8192. Together, they only contain 131k Parameters – More than 500 times the original, greatly reducing memory and computing requirements.

The disadvantage of using smaller matrices to approximate larger ones is the exact potential loss. When we multiply the smaller matrix by rebuilding the original matrix, the resulting value will not exactly match the original matrix element. This trade-off is the price we pay to greatly reduce memory and computing needs.
However, even with smaller values like k = 8, the original matrix can usually be approximated with minimal loss of precision. In fact, in practice, values as low as k = 2 or k = 4 can sometimes be used effectively.
Lola
The ideas described in the previous section perfectly illustrate Lora’s core concept. Lola represent Low-level adaptationthe term low level refers to Approximate a large number of weight matrices by assigning it to the product of two smaller matrices of lower levels k. This approach greatly reduces the number of trainable parameters while retaining the power of most models.
train
Let’s assume we have an input vector x Passed to a fully connected layer in a neural network, represented by a weight matrix before fine-tuning w. Calculate the output vector ywe just multiply the matrix by the input: Y = WX.
During the fine-tuning process, the goal is to adjust the model of downstream tasks by modifying the weights. This can be expressed as learning other matrices ΔW,so: y = (w +ΔW)x = wx +Δwx. When we see the multiplication technique above, we can now replace ΔW By multiplication BAso we end up with: y = wx + bax. As a result, we freeze the matrix wAnd solve optimization tasks to find the matrix one and b Completely included parameter ratio ΔWWoolen cloth
However, directly calculate multiplication (ba)x Due to the facts of matrix multiplication BA It’s a heavy operation. To avoid this, we can take advantage of the associated properties of matrix multiplication and rewrite the operation to B (AX). multiplication one go through x The result vector will be multiplied by b Finally, a vector is generated. This sequence of operations is faster.

Lora also offers some benefits when it comes to backpropagation. Although the gradients of individual neurons still perform almost the same operations, we now deal with fewer parameters in the network, which means:
- We need to calculate fewer gradients one and b More than originally needed w.
- We no longer need to store a huge gradient matrix w.
Finally, calculate ywe only need to add the calculated WX and BAX. There is no difficulty here, as adding matrices is easy to parallel.
As technical details, before fine-tuning, the matrix one Initialize with Gaussian distribution, matrix b Initialize with zero. Using a zero matrix b First, make sure the model behaves the same as before, because bax = 0·ax = 0so y Still equivalent to WX.
This makes the initial stage of fine-tuning more stable. Then, during the backpropagation process, the model gradually adapts to its weight one and b Learn new knowledge.
After training
After training, we compute the optimal matrix one and b. All we have to do is multiply them to calculate ΔWand we then add it to the trailer’s matrix w Obtain final weight.
Matrix multiplication BA It seems like a heavy operation that we can only perform once, so it shouldn’t be too much for us! Also, after adding, we no longer need storage one,,,,, bor ΔW.
subtle
While Lora’s idea seems encouraging, there may be a question: Why can’t we directly represent y during normal training for neural networks BAX Instead of using heavy matrix w calculate Y = WX?
Only use issues BAX is that the model will have a lower capability and may not be sufficient to enable the model to learn effectively. During training, the model needs to learn a lot of information, so naturally a lot of parameters are required.
In Lora Optimization, we treat WX A prior knowledge as large models and explain ΔWX= BAX As task-specific knowledge introduced during fine-tuning. Therefore, we still cannot deny w In the overall performance of the model.
adapter
To study LLM theory, it is important to mention “adapterThis appears in many LLM papers.
In the background of Lora adapter is a combination of matrices A and B used to solve a specific downstream task of a given matrix W.
For example, let’s assume that we have trained a matrix w Therefore, the model is able to understand natural language. We can then perform several independent LORA optimizations to adjust the model on different tasks. As a result, we obtain several pairs of matrices:
- (a₁, b₁)– Adapter for performing question-asking tasks.
- (one₂,b₂)– Adapter for text summary issues.
- (one₃,b₃)– Accept the adapter developed by chatbots.

Given this, we can store a matrix and have as many adapters as possible for different tasks we want! Since the matrices A and B are small, they are easy to store.
Real-time adapter ajustement
The great thing about adapters is that we can switch them dynamically. Imagine a scenario where we need to develop a chatbot system that allows users to select the response of the robot that should be based on the selected character, e.g. Harry Potterone angry Birdsor Cristiano Ronaldo.
However, system restrictions may prevent us from storing or fine-tuning three separate large models due to their larger size. What is the solution?
This is where the adapter is doing the rescue! All we need is a large W and three separate adapters, one for each character.

We only keep the matrix w and three matrix pairs: (a₁, b₁),,,,, (a₂, b₂),,,,, (a₃, b₃). Whenever the user selects a new character for the bot, we only need to pass the wand (aᵢ, bᵢ). As a result, if we need to add new characters in the future, we will get a very good system!
Qlora
Qlora is another popular term whose difference from Lora is only in its initials, ask,represent”Quantification“. the term”Quantification” refers to the reduction in the number of bits used to store the weight of a neuron.
For example, we can say that the neural network weight is a float that requires 32 bits per single weight. The idea of quantization involves compressing neural network weights to smaller accuracy without significant losses or impact on the performance of the model. So we can discard several bits using only 32 bits, for example, only 16 bits.

Speaking of Qlora, the quantized matrix W is used to reduce its weight magnitude.
*Bonus: Prefix adjustment
Prefix adjustment It’s an interesting alternative to Lora. The idea also includes using an adapter to complete different downstream tasks, but this time the adapter is integrated into the attention layer of the transformer.
More specifically, during training, all model layers are frozen, except adding the attention layer to some embedded prefix levels. Compared to Lora, prefix adjustment does not change the model representation and generally, it has fewer trainable parameters. As mentioned earlier, to consider the prefix adapter, we need to perform the addition, but this time there are fewer elements.
Unless very limited computation and memory limits are given, Lola adapters are still preferred in many cases compared to prefix tuning.
in conclusion
In this article, we examine advanced LLM concepts to understand how large models can be adjusted efficiently without computational overhead. Lora’s elegance of compressing weight matrix through matrix decomposition not only allows the model to train faster, but also requires less memory space. Additionally, Lora is a great example of how to demonstrate the idea of adapters that can be flexibly used and switched to downstream tasks.
Most importantly, we can add a quantization process to reduce the number of bits required to represent each neuron to further reduce memory space.
Finally, we explore another alternative called “prefix tuning” that is the same as the adapter but does not change the model representation.
resource
Unless otherwise stated, all images are by the author.



